Это один из наиболее интересных математических методов, позволяющий описать влияние случайных процессов. Система подходит и активно используется в различных научных областях, но также применяется и в спортивном беттинге, объясняя случайность исхода в ставках и оказываемую ею связь на эффективность игроков букмекерских контор с математической точки зрения.
Когда появился метод Монте Карло?
Несмотря на то, что использование случайных величин в различных задачах применялись уже достаточно давно, широкую известность и свое название система обрела только летом 2013 года. Тогда в одном из казино Монте Карло, городе, расположенном в небольшом княжестве Монако в Европе, произошел курьезный случай – в игре в рулетку шарик 26 раз подряд выпадал на черную ячейку. Большинство игроков в тот день сильно разорились, так как были убеждены, что в следующий раз шарик непременно окажется теперь уже в красной лунке. Удивительное стечение обстоятельств, не правда ли? Ведь математическая вероятность такой серии по примерным подсчетам составляет 1 к 67 млн.
Математическое представление системы
Метод Монте Карло описывает какое влияние на процесс оказывает случайность с помощью большого количества выборок из чисел, сгенерированных непредвиденным образом. Такой способ может оказаться полезен бетторам, которые слабо владеют математической статистикой в целом и отдельными методиками из этой дисциплины.
Математическая эффективность ставок
Для начала проанализируем насколько пари могут быть выгодными при многократном их заключении, если использовать один и тот же коэффициент и одинаковую сумму ставки. Представим, что мы делаем 100 одинаковых ставок. Для расчетов воспользуемся математическим ожиданием. Аналитики букмекерской конторы уже рассчитали за нас вероятность наступления исхода в коэффициентах, однако нам потребуются «отчищенные» от маржи значения котировок. Узнать, как рассчитывается маржа можно здесь. Зная маржинальную величину букмекера несложно преобразовать рыночный коэффициент в «отчищенный».
Возьмем несколько матчей и занесем полученные при расчетах математические преобразования в таблицу. Важно понимать, что для точности эксперимента стоит использовать большое количество событий (желательно несколько тысяч), но в нашем примере мы ограничимся лишь несколькими. Последний столбец информирует о том, какой процент прибыли получит беттор, делая 100 одинаковых ставок суммой 1 у.е. с идентичными котировками на каждый из представленных матчей.
| Матч | Ставка | Рыночный коэффициент | «Очищенный» коэффициент | Ожидаемая прибыль, % |
| Манчестер Сити – Манчестер Юнайтед | П1 | 1,74 | 1,60 | 9,62 |
| Арсенал – Эвертон | П1 | 1,98 | 1,93 | 2,96 |
| Барселона – Валенсия | П2 | 7,30 | 7,27 | 2,2 |
| Боруссия Дортмунд – Бавария | Х | 4,40 | 4,13 | 5,6 |
| ПСЖ – Марсель | П2 | 7,10 | 6,50 | 8,85 |
| Зенит – Динамо | П1 | 1,62 | 1,55 | 5 |
Для примера посчитаем ожидаемую прибыль для футбольной встречи «Манчестер Сити – Манчестер Юнайтед»:
- Переводим «чистый» коэффициент в вероятностное значение: 1 / 1,60 = 0,625 или 62,5 %. Это означает, что, делая 100 одинаковых ставок мы предполагаем получить примерно 63 из них выигрышные.
- Чистый доход с выигрышных пари: (1,74 * 1 – 1) * 63 = 46,62 у.е.
- Убыток с проигрышных пари: (100 – 63) * 1 = 37 у.е.
- Итоговая прибыль со 100 ставок: 46,62 – 37 = 9,62 у.е. или 9,62 % от общего оборота.
Аналогичным образом вычисляется ожидаемая прибыль и для остальных событий. Средняя доходность в примере получилась: (9,62 + 2,96 + 2,2 + 5,6 + 8,85 + 5) / 6 = 5,705 %. Как видим, наша модель информирует нас о том, что при многократном заключении пари мы будем получать положительную прибыль. Но так ли это будет в действительности? Если нет, то насколько сильно невезение будет оказывать влияние на нашу систему? На этот вопрос мы получим ответ, применив методологию Монте Карло и сравним с этой.
Как использовать Монте Карло в ставках на спорт?
Произвести расчет с помощью системы Монте Карло достаточно просто применив Excel или язык программирования R, который используют статисты. Для начала внесем в нашу таблицу вероятность выигрыша ставки по каждому матчу. Это отношение 1 к «очищенному» коэффициенту без маржи. Данные можно взять из прошлой таблицы.
| Матч | Ставка | «Очищенный» коэффициент | Вероятность выигрыша (1 / коэффициент) | Случайное число | Прибыль |
| Манчестер Сити – Манчестер Юнайтед | П1 | 1,60 | 0,625 (1 / 1,60) | 0,459 | 0,60 у.е. (1,60 * 1 – 1) |
| Арсенал – Эвертон | П1 | 1,93 | 0,518 | 0,13 | 0,93 у.е. |
| Барселона – Валенсия | П2 | 7,27 | 0,138 | 0,77 | -1 у.е. |
| Боруссия Дортмунд – Бавария | Х | 4,13 | 0,242 | 0,619 | -1 у.е. |
| ПСЖ – Марсель | П2 | 6,50 | 0,154 | 0,481 | -1 у.е. |
| Зенит – Динамо | П1 | 1,55 | 0,645 | 0,267 | 0,55 у.е. |
В столбце «Случайное число» находятся сгенерированные случайным образом числа от 0 до 1, выполненные с помощью Excel или R. Если полученное значение оказывается меньше нашей вероятности, то мы фиксируем прибыль в последнем столбце, как если бы сумма пари соответствовала 1 у.е. По сути таким образом мы сравнивали нашу математическую вероятность со случайной. Далее просуммируем полученные прибыли и получим -0,92 у.е.
Теперь с помощью софта повторите процедуру с генерацией случайных цифр и снова зафиксируйте полученную доходность. Для полноты картины повторите данную процедуру сто тысяч раз. Для этого программе потребуется определенное время. Затем посчитайте среднее арифметическое доходности от всех итераций. В данном эксперименте было получено примерное значение прибыльности 4,04%, что достаточно близко от результата, выполненного через математическое ожидание в начале статьи (5,705 %). Но также можно видеть и широкий разброс данных от -12,22 % до 23,27 %. Почти 17 % итераций оказались убыточными. Это говорит нам о том, что влияние случайности на наш эксперимент оказалось не таким и высоким. Мы даже можем посчитать вероятность получения того порогового значения прибыли, на которую рассчитывали. Информация по проведенному эксперименту представлена ниже на графике с нормальным распределением:
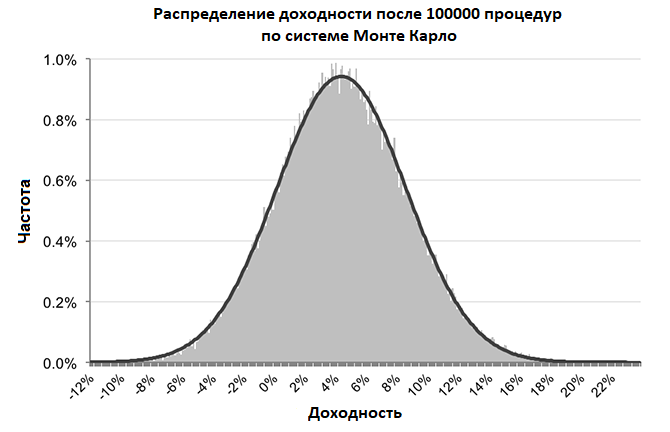
Вывод
Система Монте Карло с помощью большого количества выборок, каждое из которых состоит из набора случайных числовых значений, позволяет просчитывать нам процент вероятности получения того уровня доходности, которое мы закладываем в нашу стратегию ставок. Чем больше моделирований в нашем эксперименте, тем точнее будет наш результат. Данный метод лишь характеризует степень везения, оказываемое на сделанные пари и, конечно же, не учитывает те многочисленные факторы, которые применяются бетторами при прогнозировании исходов.
Автор: Alex